遊ぶ数学 三角形の合同条件はなぜ3つ?証明問題をわかり こんにちは、ウチダショウマです。 今日は、中学2年生で習う関門 「三角形の合同条件」 について、まずは図形の合同を確認し、次に合同条件を用いる証明問題を解き、またコラム的な内容も考察していきます。 自分用に作ってたので、字が汚いです いろんな合同条件などがあり、ゴチャゴチャになりがちなので、まとめてみました! 学年 中学2年生, 単元 平行と合同の利用,三角形,四角形, キーワード 中学2年 数学 照明 合同条件 特に合同条件はなぜ成り立つのかわからない人も多いと思います。そこで今回は言葉の意味をわかりやすく説明していきたいと思います。合同条件まずは合同条件です。2つの三角 難関高校に受かるための数学 苦手だったからこそ苦手な受験生たちにとってわかりやすい数学を 合同条件

三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学
数学合同条件
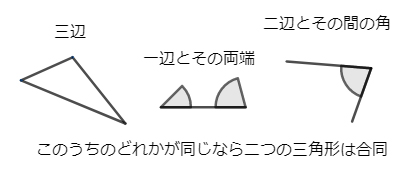
数学合同条件-合同条件」の問い 藤原大樹.(19).「公開授業 第2 学年 数学科学習指導案『直角三角形の合同条件』」.日本数学教育学会研究部中 学校部会.第4 回数学授業づくり研究会.p3639三角形が完全に決定される場合 1:三辺の長さ a, b, c a,b,c a,b,c が与えられた場合 余弦定理から角 A, B, C A,B,C A,B,C が求まります。 これは,「三辺の長さがそれぞれ等しい三角形は合同である」という事実と対応しています。 2:二辺の長さ




合同条件 合同成立的条件
このページへリンクしているページ を見つけたら、リンクを適切な項目に張り替えて下さい。 「 https//jawikipediaorg/w/indexphp?title=合同&oldid= 」から取得 カテゴリ 曖昧さ回避 同値 (数学) 隠しカテゴリ すべての曖昧さ回避 証明に使う"合同条件"性質"まとめました。 良かったら、最後まで見てください! 学年 中学2年生, 教科書 未来へひろがる数学2 啓林館, 単元 証明, キーワード 数学証明,合同な図形と証明, 三角形の合同条件3つ まずはイメージしてみよう!合同条件は、この3つだ。 三角形の合同条件① 3組の辺がそれぞれ等しい。 3つの辺が、ぜ~んぶ同じ長さだったら全く同じ三角形になるよね?? 三角形の合同条件② 2組の辺とその間の角がそれぞれ等しい。
数学: 数学1 年 ,数学2 年,数学3 年 を掲載しておりますが,印刷はできないように設定しております 仮定と結論,逆,合同条件 問題 次の①~④のことがらの中から逆が正しいものをすべて選び,番号を書け。 ① b整数 a, で,aもb も偶数ならば,abは偶数である。 ② ABC で,AB岐阜数学教育研究 09, Vol8, 115 三角形の合同条件を題材とする授業の提案と実践 淺井洋佑1, 愛木豊彦2 新学習指導要領の改訂の基本方針などから, 今後, 生徒の数学的な思考力・表現力を育 成することが, これまで以上に必要とされることが予想できる。そこで, 証明を通して, 数 ここで三角形の合同条件を思い出して! 忘れた人はココ:三角形の合同条件 すると、 2組の辺とその間の角がそれぞれ等しい ので、 ade≡ acbとなる。 合同な図形では、対応する辺の長さが等しいので bc=edである。 ・・・(ここまでが答え)
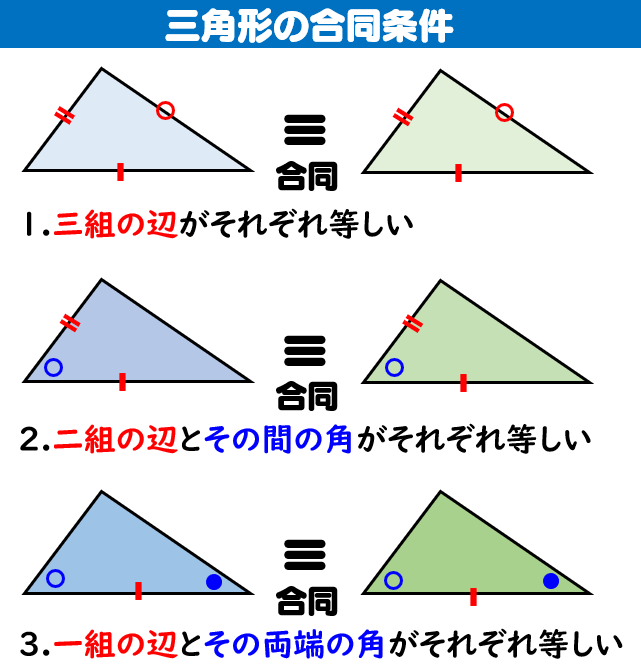
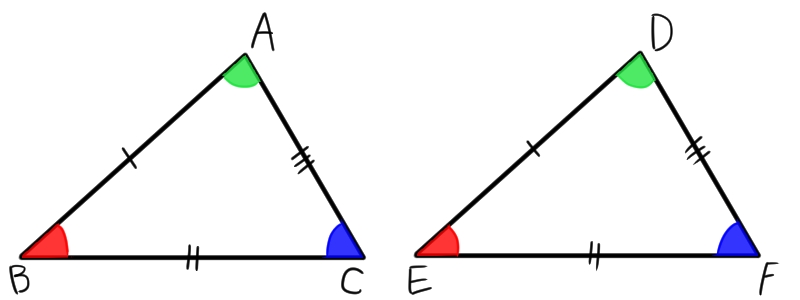
数学 三角形の合同条件と証明問題の解き方|数学fu 中学2年で学習する「平行と合同」単元のポイントまとめと証明のしかた、書き方をお伝えします。 中学2年生でテストで得点が下がる人が急増するのがこの「平行と合同」分野です。 角度の問題は計算できれば良いですが、大切な用語が増合同条件が分かれば、2つの三角形が合同かどうかを数学的に判断することが出来るようになります! そもそも合同って何だっけ? と思う方でも読み進められるように、 合同 について復習できる内容を記事内に入れていますので、良ければ最後まで読み進めていってみてください。三角形の合同条件 三角形が合同であるためには、次の3つの条件のうち1つでも満たせばOKです。 3つの辺の長さがそれぞれ等しい この図形の場合 ・ab=de ・bc=ef ・ca=fd 2つの辺の長さと、その間の角の大きさがそれぞれ等しい
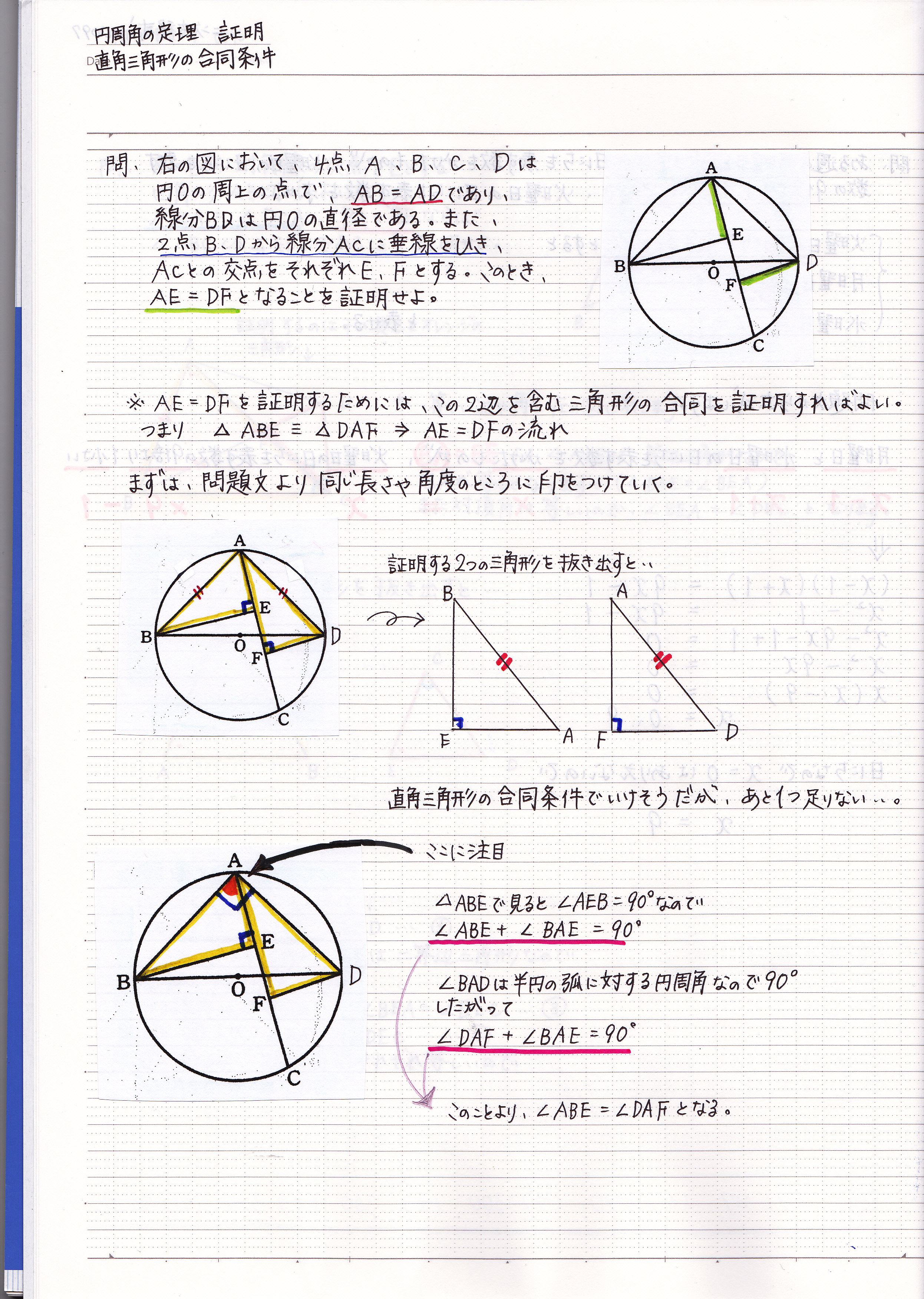



図形の証明 合同 現役塾講師のわかりやすい中学数学の解き方




暗記必須 三角形の合同条件を見やすい図で一発理解しよう 高校生向け受験応援メディア 受験のミカタ
直角三角形の合同条件 1 斜辺と 1 1 つの鋭角がそれぞれ等しい。 2 斜辺と他の 1 1 辺がそれぞれ等しい この 2 2 つは暗記してください。合同数の問題 合同数の問題とは、どのような数が合同数になるかという問題である。これは数学上の未解決問題の一つである。 定義より明らかに、合同数は正の有理数である。また、辺の長さが (a, b, c) である直角三角形の面積が S であるとき、(k a, k b, k c) の面積は k 2 S であることから三角形の合同条件 3組の辺がそれぞれ等しい。 2組の辺とその間の角がそれぞれ等しい。 1組の辺とその両端の角がそれぞれ等しい。
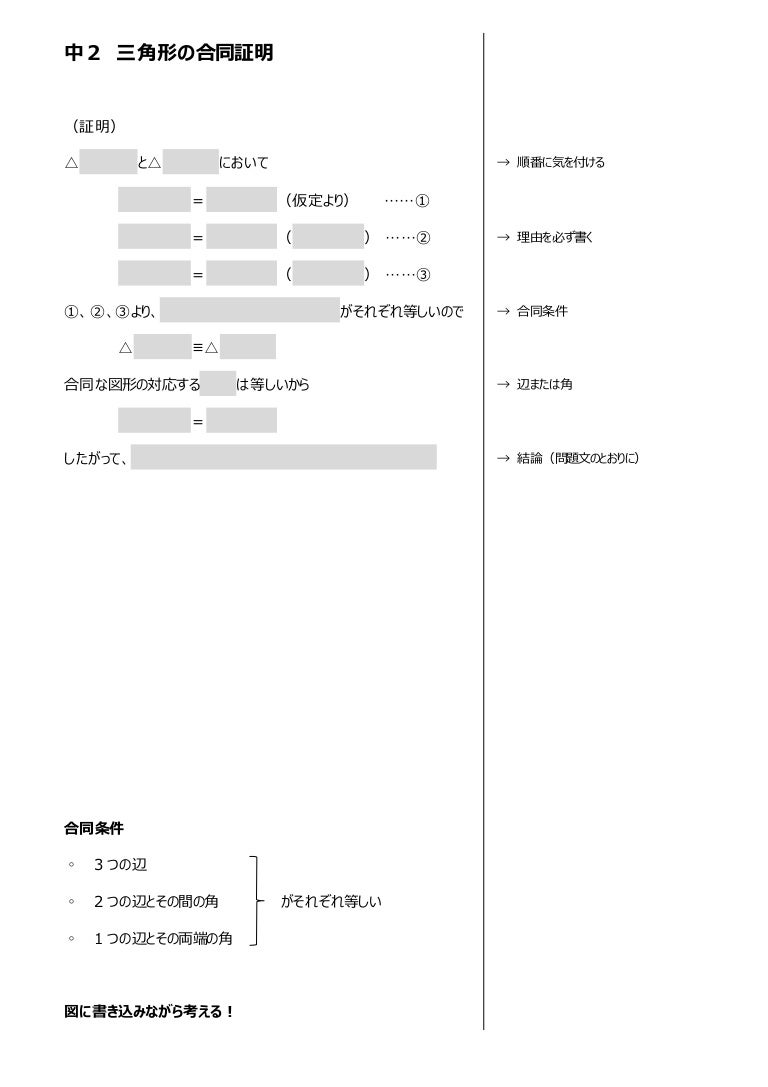



三角形の合同証明 中2数学 幾何




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学
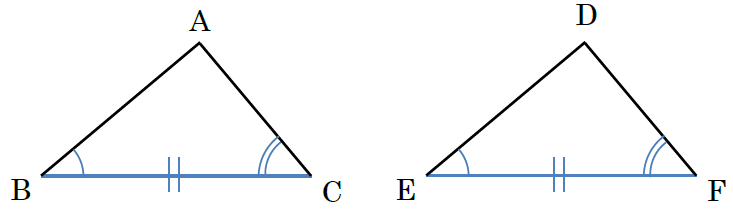
この映像授業では「中2 数学 合同4 合同条件(1辺と両端角)」が約10分で学べます。問題を解くポイントは「1組の辺とその両端の角が中学校数学 三角形の合同条件と証明問題の解き方 管理人 2月 , 19 「図形の合同」については小学校の算数で少し習ったと思いますが、中学校ではさらに「合同条件」や「合同の証明」などを習います。 今回は三角形の合同条件や三角形の合同を証明する問題の解き方について見ていき 三角形の合同条件 一方の図形を移動させて他方の図形と完全に重なる時 、この2つの図形の関係を 合同 と言います。




三角形の合同条件 Youtube




暗記必須 三角形の合同条件を見やすい図で一発理解しよう 高校生向け受験応援メディア 受験のミカタ
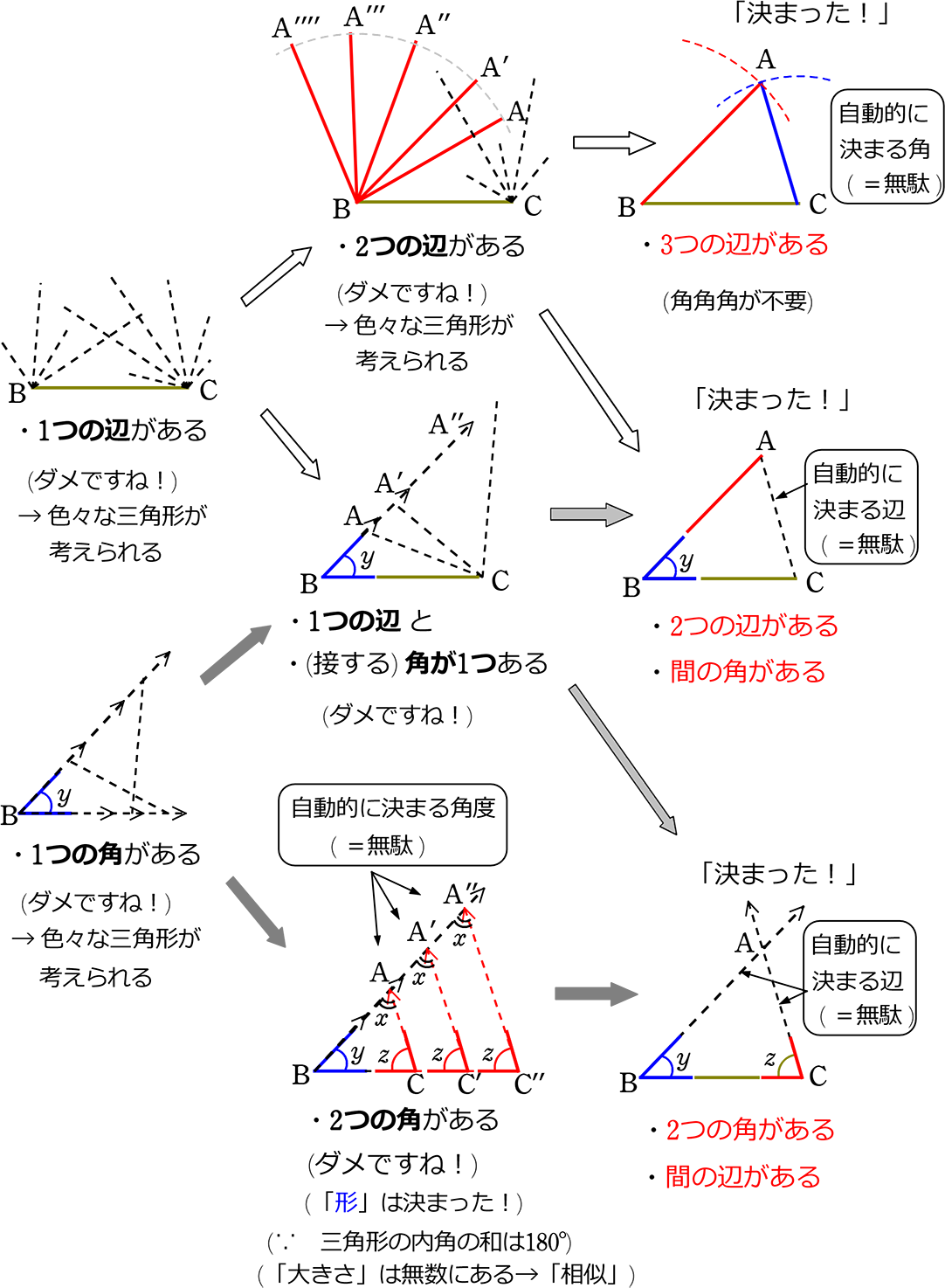
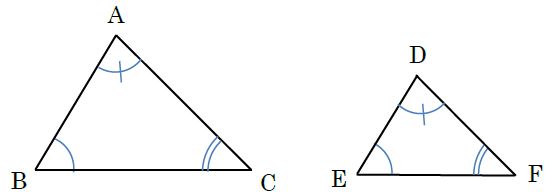
中学数学教科書「未来へひろがる数学」Q&A 三角形の合同条件の記述が,以前の教科書と変わっていますが,その理由を教えてください。 三角形の合同条件の記述 (2年p96)について,平成24年度教科書から次のように変更しております。 旧教科書 (1合同关系是一个等价关系,也就是说满足: 1、反身性:任意矩阵都与其自身合同; 2、对称性:A合同于B,则可以推出B合同于A; 3、传递性:A合同于B,B合同于C,则可以推出A合同于C; 合同条件1「3つの辺の長さがそれぞれ等しい」 「3つの辺の長さ」 がすべて等しいっていう条件は合同条件だ。 この条件を満たす三角形たちは合同である、ってことが言えるわけね。 たとえば、次の2つの ABCと DEFを想像してみて。 AB = 6 cm BC = 8 cm AC = 7 cm と、 DE= 6 cm




高等数学上12 13考研数学辅导13版f二次型下载 Word模板 爱问共享资料
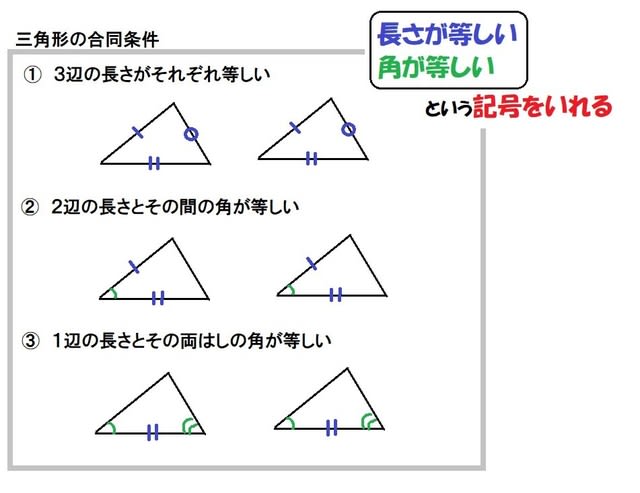



合同な図形 小5 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support
② 三角形の合同条件 ※以後は「要件」という言葉を、数学に合わせて「条件」と言いますね 基本、「合同」の条件は、 ① 全ての辺の長さが同じ、 かつ ② 全ての角の大きさが同じ という事実を集められれば、「証明」ですね! 例えば、 Hypotenuse Leg Theorem 日本の中学数学2の教科書には,三角形の合同条件(triangle congruence theorems/postulates)は次の3つが書かれています. 加えて直角三角形の合同条件として以下の2つが述べられています. しかし,③を言いかえると「2組の角とその間の辺が合同式において,足し算,引き算,かけ算は普通の等式と同様に行ってOKですが,割り算は a a a と n n n が互いに素という条件がつきます(超重要)。




三角形の合同条件のなぜ 中2数学 Youtube




中2数学 三角形の合同条件2 2辺とその間の角 例題編 映像授業のtry It トライイット
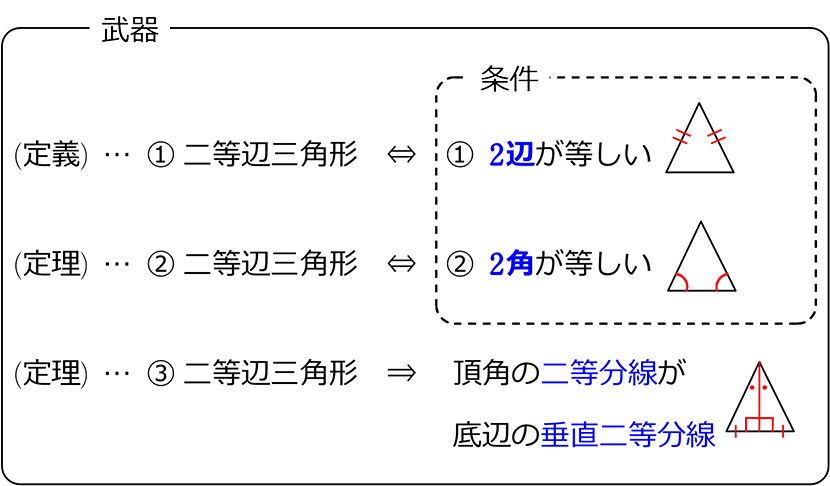
因工作需要,数学学院现面向校内外公开招聘行政业务岗合同制人员1名,具体要求如下: 一、岗位职责1 协助做好学院办公室行政管理相关工作;2 自觉服从学院岗位调整与安排;3 做好学院领导交办的其它工作。二、招聘条件1具有全日制本科生及以上学历,有较好的语言表达能力和文字写作能力。合同条件 合同の証明 二等辺三角形 直角三角形 三角形 例題 三角形の合同証明1 三角形の合同証明2(辺の共通) 三角形の合同証明3(角の共通) 合同証明応用(直線と内角の和) 合同証明応用(角の引き算) 二等証明とは? 証明はハンバーガーだ1(1行目の書き方のコツ) 証明はハンバーガーだ2(中身の書き方のコツ) 証明はハンバーガーだ3(結論の書き方のコツ)



中2数学 直角三角形の合同条件と証明問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




上数学合同条件 ニスヌーピー壁紙
摘要: 考研数学里关于矩阵的相似、合同、等价的关系有时令大家头晕脑胀,就需要大家对它们的性质、定义要更加清楚,得分才不难。 接下来一起看看三者的纠缠吧。 关于矩阵的相似、合同、等价的关系 总结起来就是一句话 相似必合同,合同必等价数学で 逆 が正しくない場合があるのは、けっして文字式の分野だけではなく、図形の問題でも、逆が正しくない場合がある。 「 abcと defの対応する角度3つがそれぞれ等しいなら、その三角形が合同である」は正しくない。




中2の証明問題を解く上で 必要な知識をまとめました プリントダウンロードできます 東大に文理両方で合格した男が綴る 受験の戦略




17考研数学 二 中如何判定矩阵合同关系 文都考研网




合同条件 合同成立的条件




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット
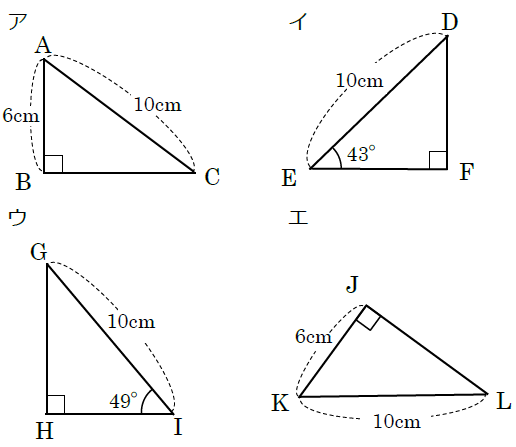



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




中2数学 合同条件と定義 定理 性質の確認
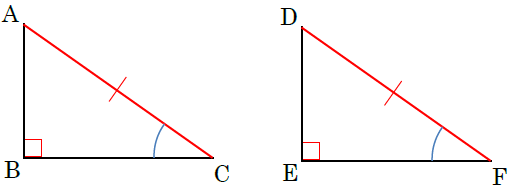



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン
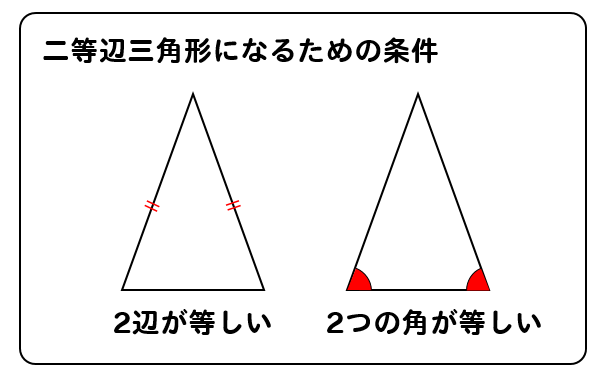



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ
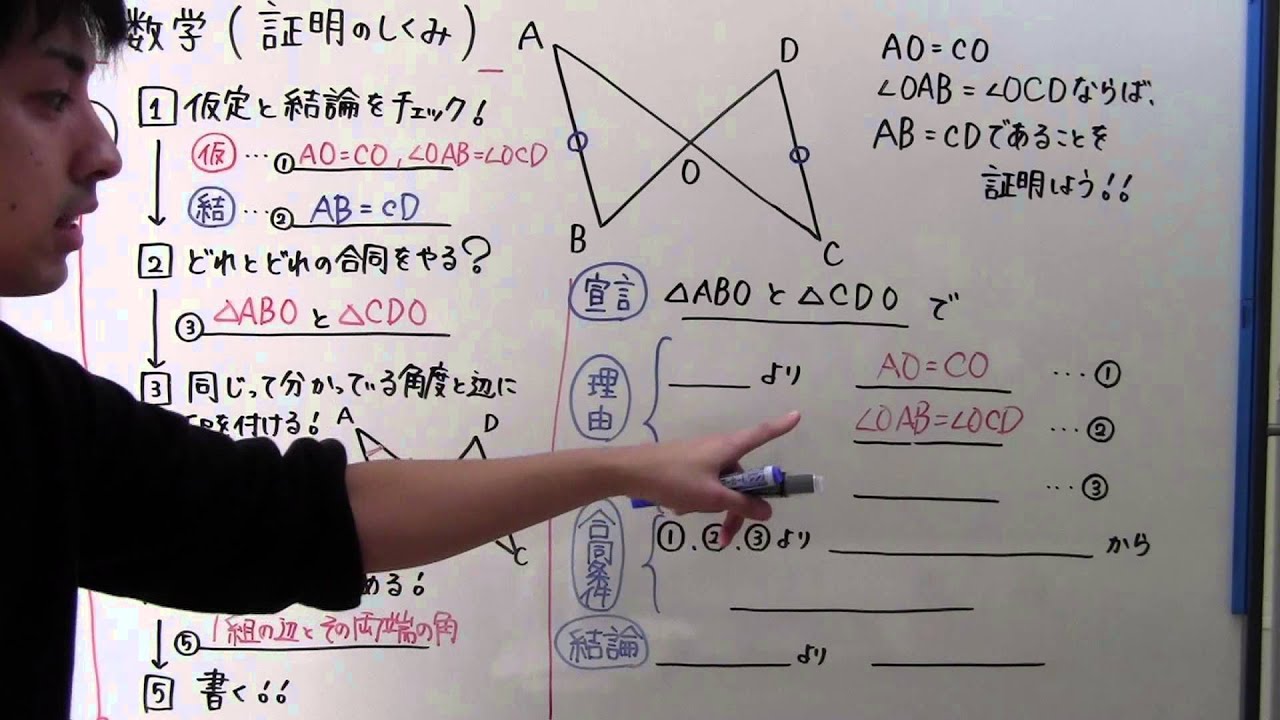



中2 数学 中2 60 証明のしくみ Youtube




菲迪克fidic文献译丛合同指南 简明合同格式 施工合同条件 生产设备和设计 施工合同条件 设计采购施工epc 交钥匙工程合同条件 虎窝淘



中学数学 図形の合同 図形の性質



上数学合同条件 ニスヌーピー壁紙




中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学



中学数学 図形の合同 図形の性質




50 素晴らしい数学相似条件 最高のぬりえ
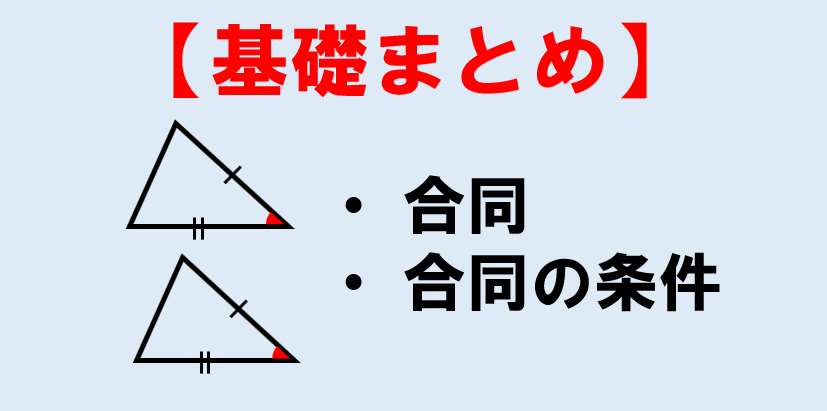



中2数学 合同 三角形の合同条件まとめ 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




数学史の視点から分析する 中学校数学 重要教材研究事典 図形編 Wataru Uegaki Amazon Com Books




合同条件 合同成立的条件
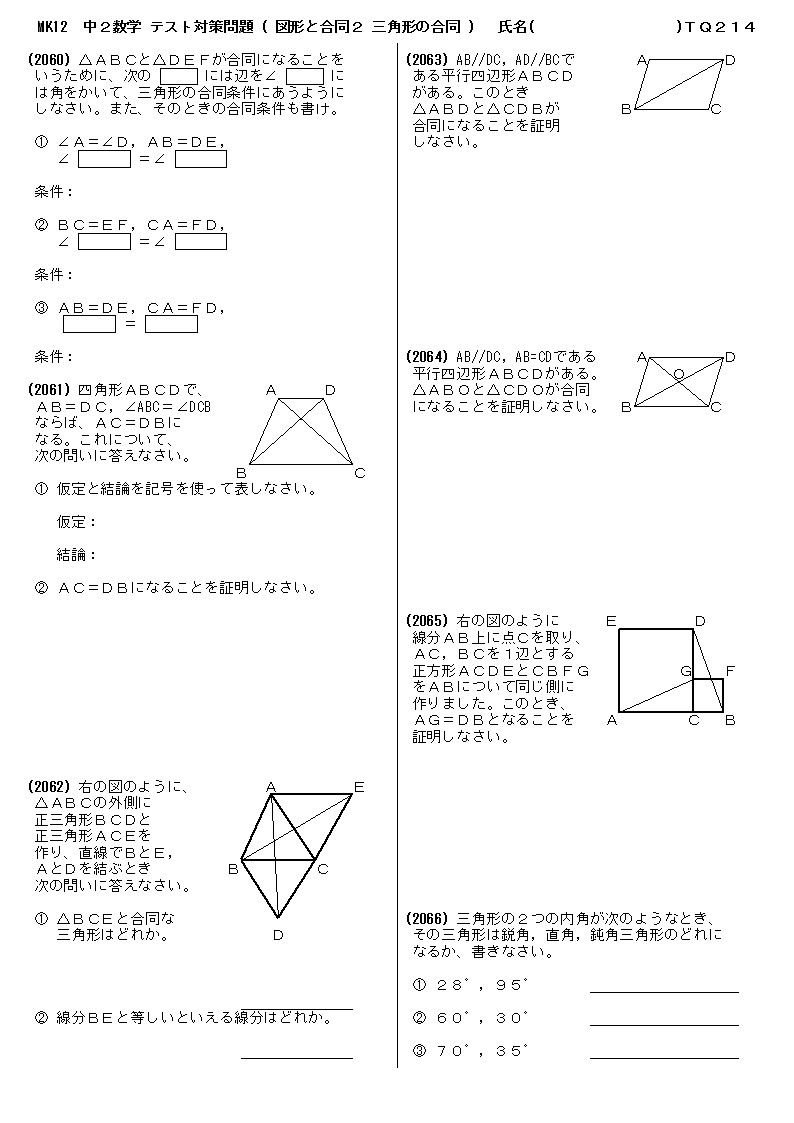



無料 中2数学 テスト対策 問題プリント 214 図形と合同2 三角形の合同



合同条件に なぜ 3つの角がそれぞれ等しいがないのかについて Yahoo 知恵袋




3分で分かる 三角形 直角三角形の合同条件とその使い方をわかりやすく 合格サプリ




三角形の合同条件と証明問題の解き方 数学fun



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




2 の直角三角形の合同条件は何ですか 理由も付けて教えて頂けると助かります Clear




暗記必須 三角形の合同条件を見やすい図で一発理解しよう 高校生向け受験応援メディア 受験のミカタ




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学



数学のアレ 何に役立つ 三角形の合同条件 同じ形の三角形を見つけて テストで5点くらいもらう 以外の使い方 1 2 ページ ねとらぼ




上数学合同条件 ニスヌーピー壁紙



三角形の合同条件と証明問題の解き方 数学fun



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン



中2数学 発展問題プリント12 図形4 三角形の合同条件 問題 224
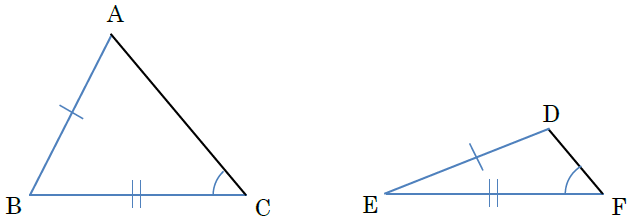



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




直角三角形の合同条件再び 中学校2年生の数学 身勝手な主張




直角三角形の合同条件とその証明 数学fun




中2 中2 数学 主要合同条件 定理 定義 中学生 数学のノート Clear




中2数学 チョー便利な直角三角形の2つの合同条件 Qikeru 学びを楽しくわかりやすく
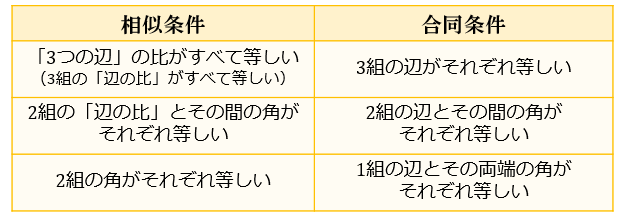



三角形の合同条件 相似条件と合同条件の違いとは アタリマエ
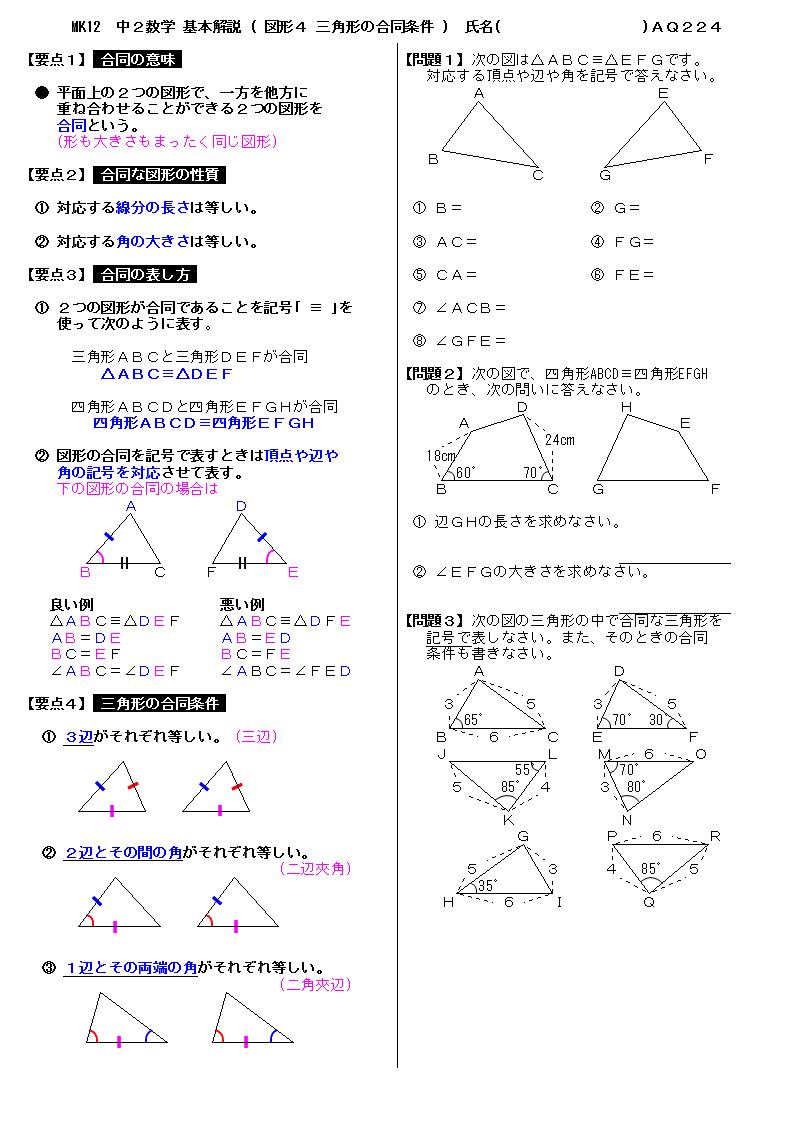



無料 中2数学 基本解説 問題プリント 224 図形4 三角形の合同条件



水木艾迪考研数学解题36计之28 等价相似与合同下载 在线阅读 爱问共享资料




三角形の合同条件 中学数学 By じょばんに マナペディア
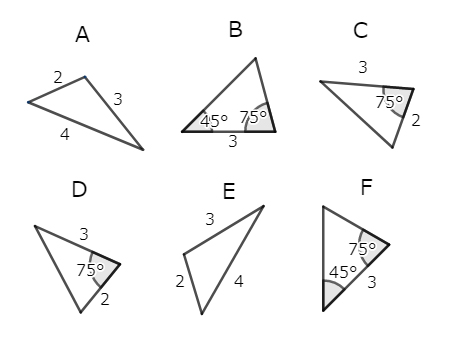



数学のアレ 何に役立つ 三角形の合同条件 同じ形の三角形を見つけて テストで5点くらいもらう 以外の使い方 1 2 ページ ねとらぼ




合同制 仲恺中学和潼湖中学再招2名控股初中数学老师 考试 笔试 应届毕业生 教师资格证 网易订阅




中学校数学 証明のコツ 直角三角形の合同条件 と その利用の仕方 を自学自習できる教材
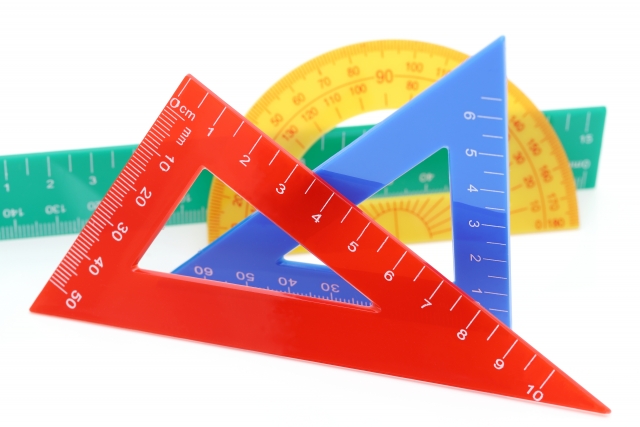



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




中学生 三角形の合同条件のノート一覧 Clear




三角形の合同条件を使った証明問題 中学2年生の問題を解こう 身勝手な主張



新高一 数学第二课 集合知识点总结及练习题 综合




直角三角形の合同条件 算数 数学が好きになりmath




中学数学より3 三角形の合同条件 身勝手な主張




三角形の合同条件 合同の証明問題と解き方のコツ リョースケ大学



上数学合同条件 ニスヌーピー壁紙




75 数学相似条件 最高のぬりえ




高一数学必修2知识点总结 Doc下载 Word模板 爱问共享资料




中2数学 三角形の合同条件3 1辺とその両端角 映像授業のtry It トライイット



Studydoctor三角形の合同条件 中2数学 Studydoctor




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




世界一わかりやすい数学問題集中2 4章 平行と合同と証明




中2数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾




中2 数学 中2 証明 中学生 数学のノート Clear



中学生です 数学について三角形の合同 相似の証明のための合同条件や直角三角形 Yahoo 知恵袋




75 数学相似条件 最高のぬりえ




中2数学 三角形の合同条件2 2辺とその間の角 練習編 映像授業のtry It トライイット
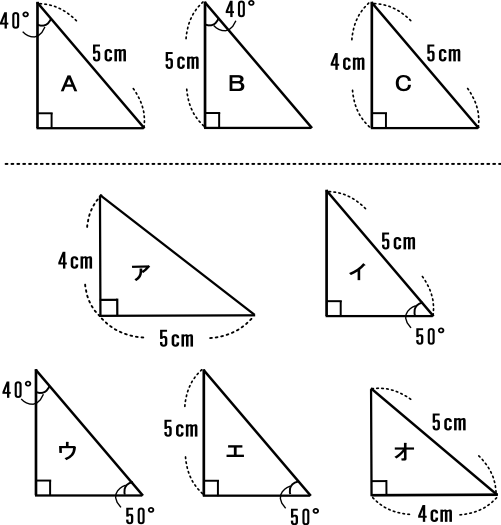



中学2年数学練習問題 直角三角形の合同条件と証明問題 図形と合同




三角形の合同条件 証明のときに絶対にしておかないといけない問題 中学や高校の数学の計算問題
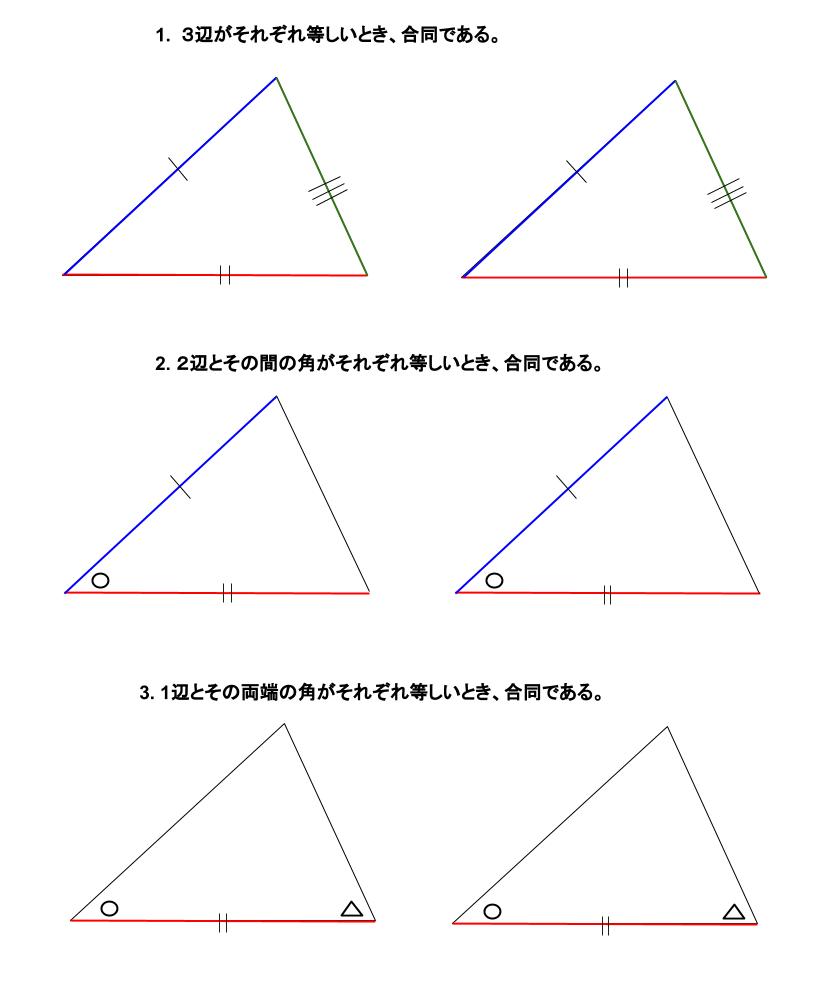



中学数学 三角形の合同条件 中学数学の無料オンライン学習サイトchu Su




21年新书设计采购施工epc 交钥匙工程合同条件 原书17年版 菲迪克 Fidic 文献译丛书国际咨询工程师联合会机械工业出版社
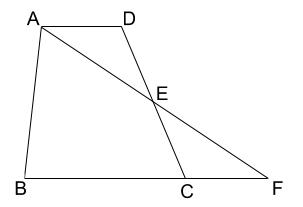



中学数学 三角形の合同の証明の利用 その1 中学数学の無料オンライン学習サイトchu Su



Studydoctor三角形の合同証明の進め方 中2数学 Studydoctor
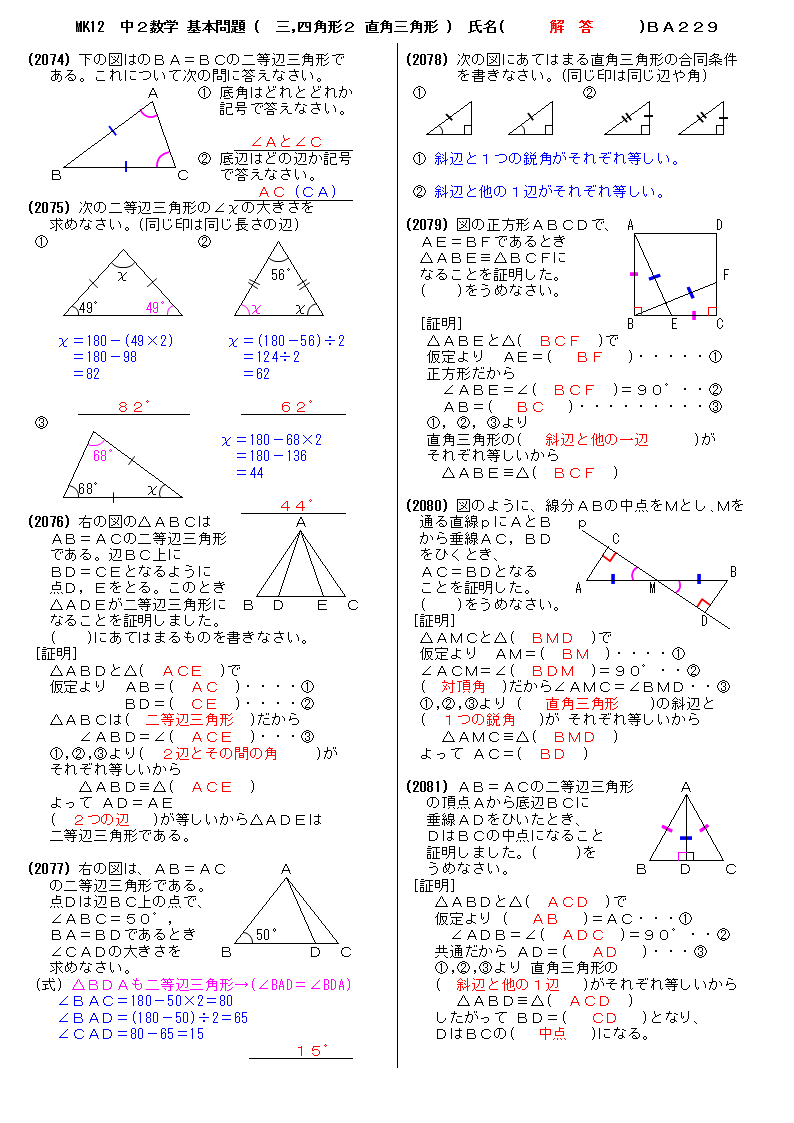



無料 中2数学 基本問題 解答プリント 229 三角形 四角形2 直角三角形



中学2年生の数学 証明 三角形の合同条件と証明の書き方 塾講師が数学をやりmath




75 数学相似条件 最高のぬりえ




三角形の合同条件はこうやって理解する 高校受験のバイブル




17考研数学 矩阵合同与相似的典型题型分析 文都考研网
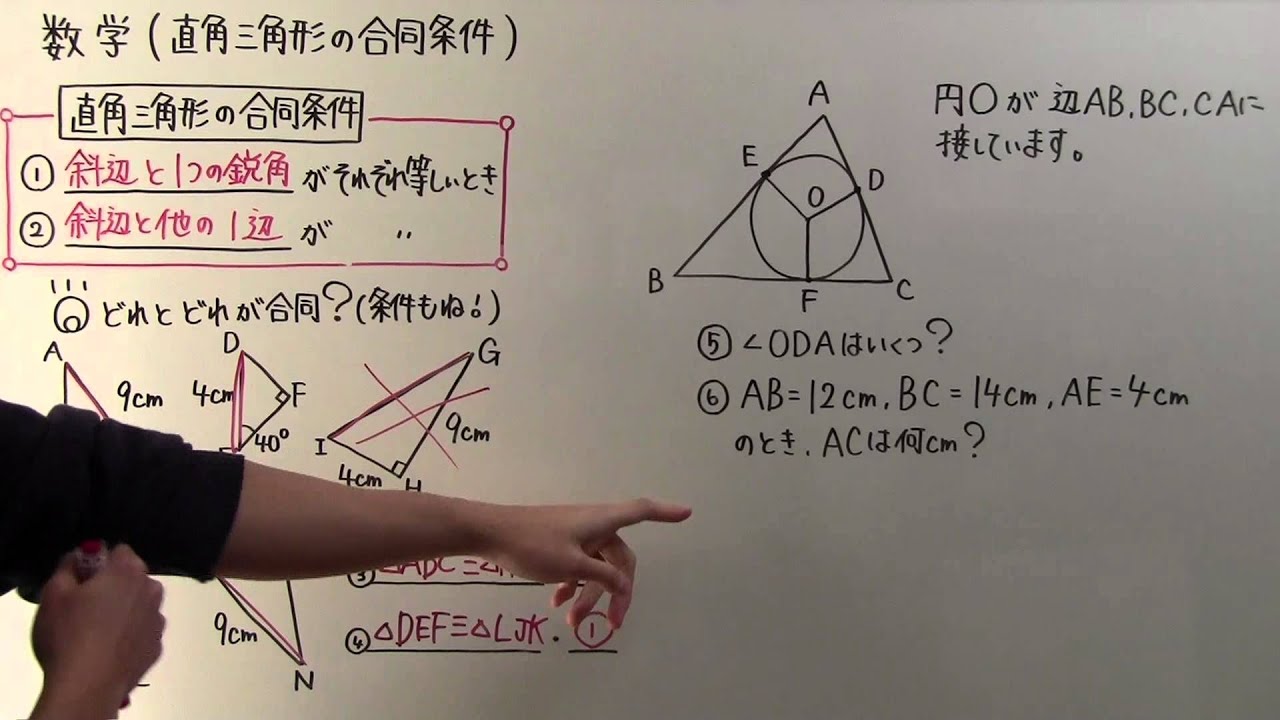



数学 中2 71 直角三角形の合同条件 Youtube




中2 数学 合同2 合同条件 3辺 10分 Youtube




直角三角形の合同条件とその証明 数学fun




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




上数学合同条件 ニスヌーピー壁紙
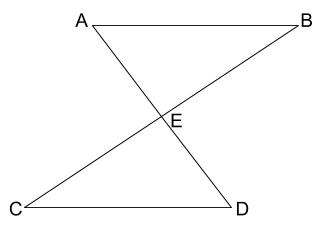



中学数学 三角形の合同条件 中学数学の無料オンライン学習サイトchu Su




三角形と四角形 三角形の合同の証明のしかた 中学数学 定期テスト対策サイト



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典




保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく
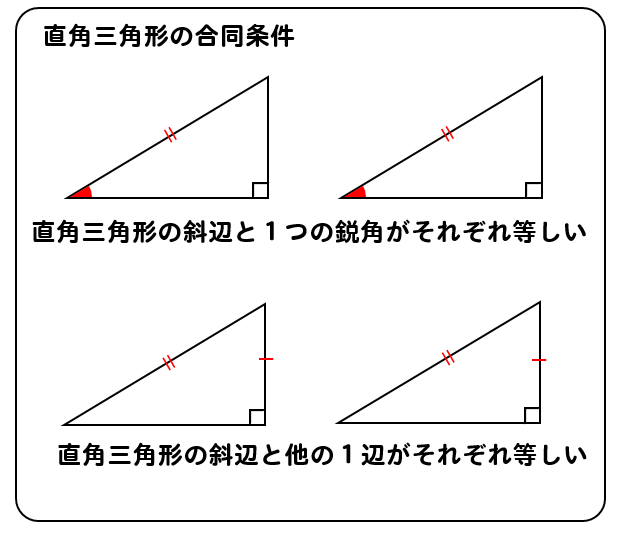



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ
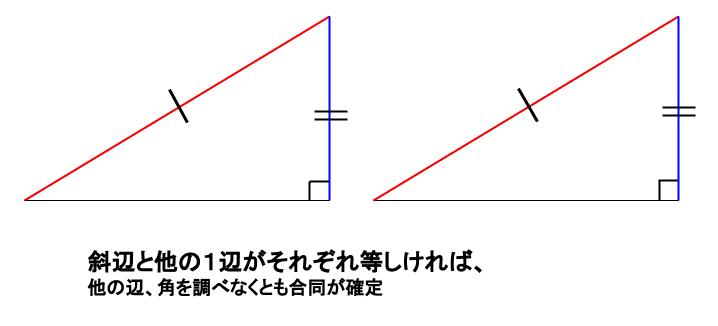



中学数学 直角三角形の合同条件 中学数学の無料オンライン学習サイトchu Su



上数学合同条件 ニスヌーピー壁紙




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学




数学 中2 56 三角形の合同 基本編 Youtube



0 件のコメント:
コメントを投稿